I. Prolonged Password

Problem Source: 2018 Asia Singapore ICPC Regionals

We visualise this problem as a tree. The root is an empty node, and it’s children are the letters of \(S\). If a node has character \(\alpha\), then the children of each node are the letters in string \(T_\alpha\). Each level of the tree represents a single application of the function \(f\), so that that the final password \(f^K(S)\) is represented by the leaves of the tree with depth \(K+2\). However, expanding the whole tree is clearly too expensive, since we can have up to \(50^{10^{15}} \simeq 10^{1698970004336019}\) letters (leaves) in the final string.

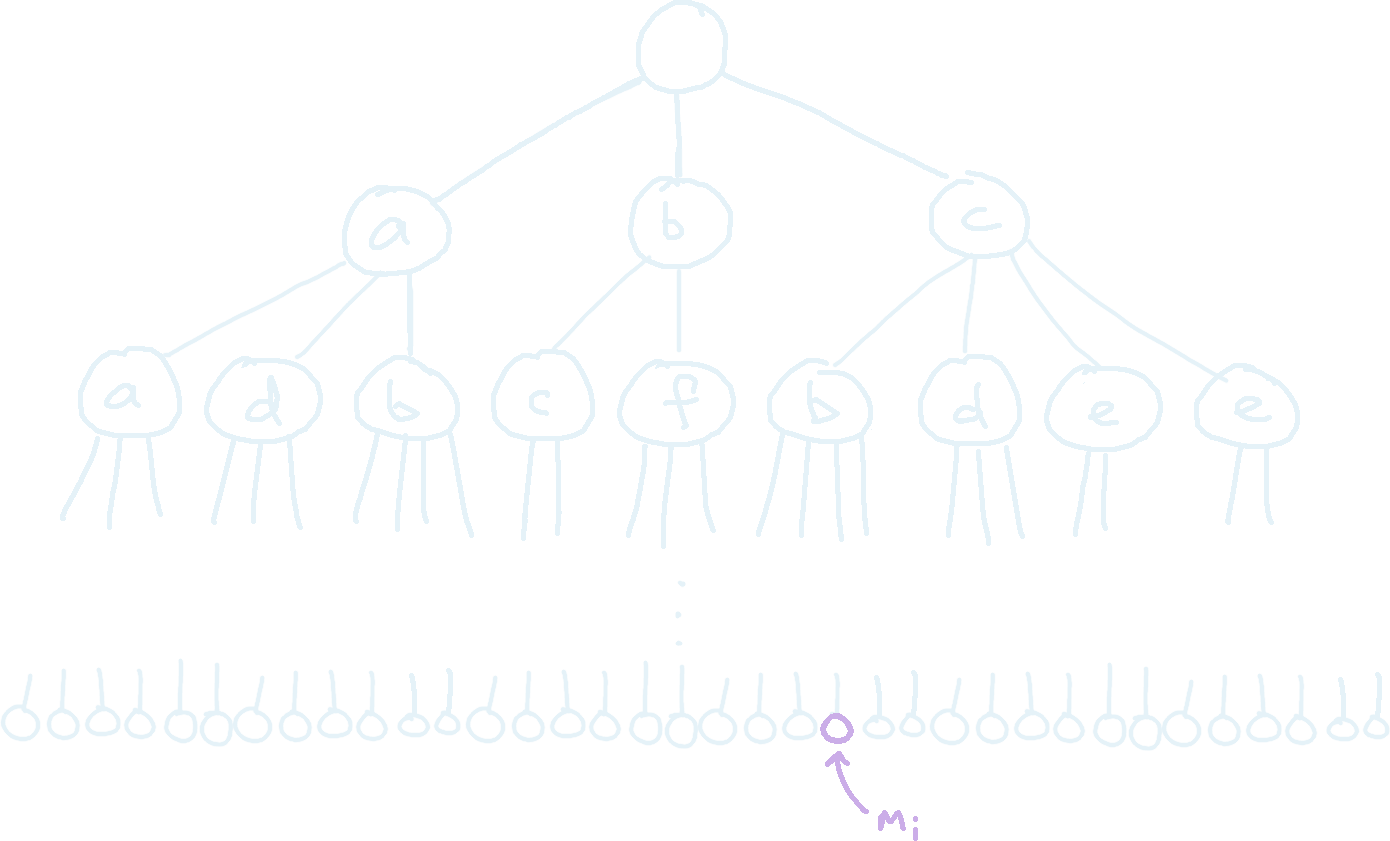
Recursive Expansion

Suppose we had a method of fksize(char c, int k), which given a character \(c\) and a number \(k\), will work out the size of \(f^k(c)\). Then a better solution would be to start at the root of the tree, and evaluate the size of each its children after \(K\) expansions. This tells us which child’s expansion houses \(m_i\), so we recurse to that child and apply the same algorithm again with \(K-1\) expansions instead. We can repeat this until we reach a leaf. This is marginally better, since we don’t have to store the whole tree, but we still have to explore at least \(\mathit{tree\ height} \times 50\) nodes, which is still too expensive given \(K\) goes up to \(10^{15}\).

One observation to make is that \(m_i \le 10^{15}\). This means that even though the tree can grow extremely large, we only care about a small fraction of the leaves to the left of the tree. Therefore, for large \(K\), at each iteration of our expansion, it is more than likely that \(m_i\) will lie in the expansion of the first character.

Recursing Down the Left

To find out how many times we should recursively expand the first character, recall that the smallest value for any \(T\) is 2, so the tallest tree that will contain all of the first \(10^{15}\) leaves has a height of \(\log_2(10^{15}) \simeq 49.82 < 50\). This tells us that no matter how big \(K\) is, all we need to do is keep recursing down the first child of the tree until we are at a depth of 50 from the end, then run our recursive expansion solution from that subtree for each \(m_i\). Furthermore, this subtree is uniquely defined by the character at it’s root. Hence, if we have a way to calculate that character, then we can also skip the entire recursion down the tree, and only deal with a tree of depth 50, which is far more managable.

Let’s define the function fkfirst(char c, int k). Given a character \(c\) and a number \(k\), it will work out the first character of \(f^k(c)\). We can solve this particular problem using knowledge of vortex graphs. Let each character have a node representing it in the graph. Each character will have an edge pointing towards the first letter in its corresponding \(T\). Then, recursing down the first child of the tree \(K\) times is equivalent to following the singular outgoing edge from each node \(K\) times.

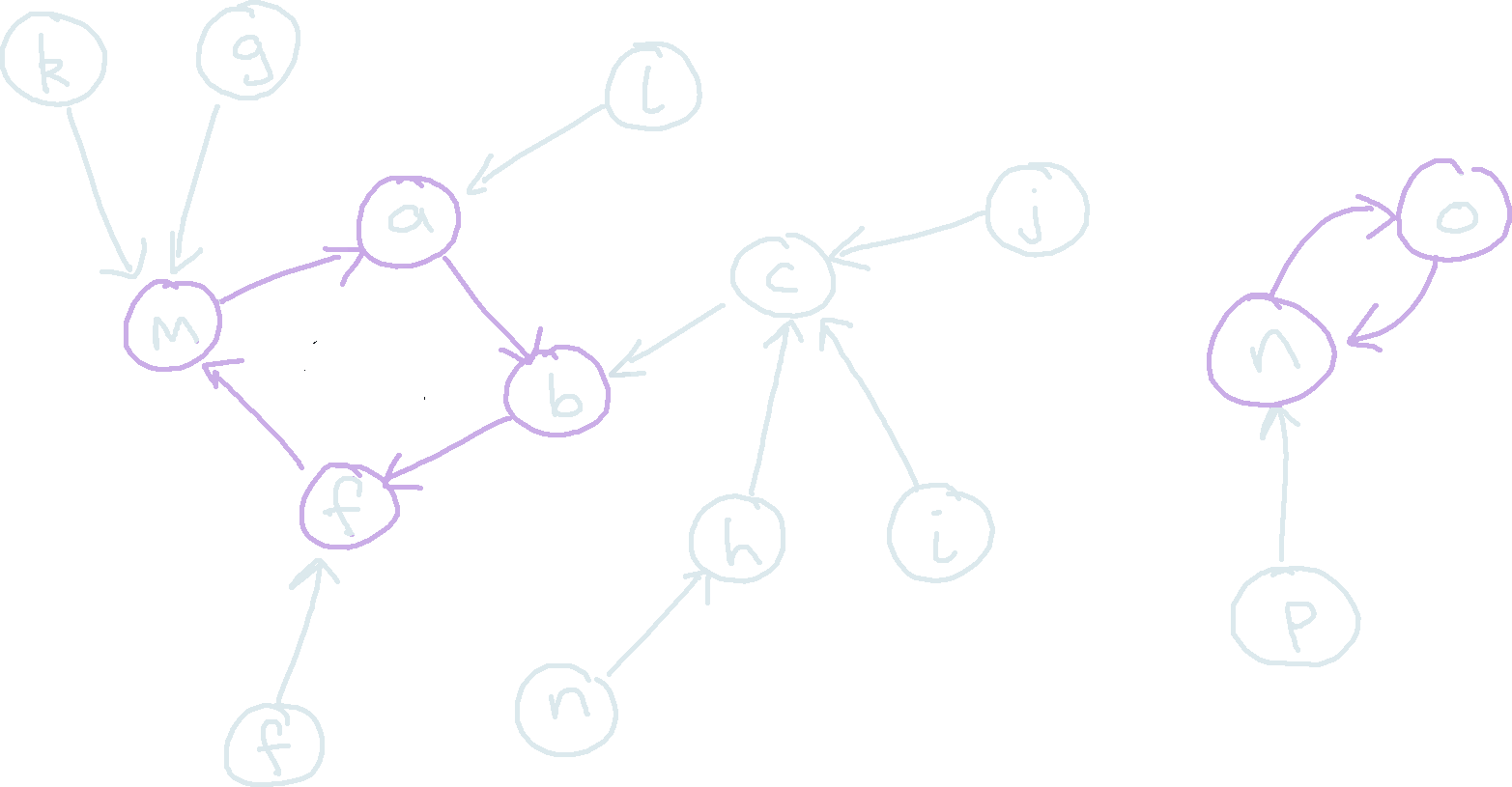
Since each node has exactly one outgoing edge, this results in a vortex graph. A vortex graph essentially looks like a series of cycles, with trees hanging off of it. No matter which node we start at, after following the edge enough times, we will always be caught in an infinite cycle. We can use a DFS to locate each cycle and store it’s length. Then, to calcualte fkfirst(char c, int k), we simply expand \(c\) until we are caught in a cycle, then use the fact that the cycle repeats itself periodically to calculate the final position after \(k\) expansions. This can be done in \(O(26)\) constant time.

Predicting the size after \(k\) expansions

Finally, we describe how to implement fksize(char c, int k). We can implement this using dynamic programming. Let \(dp[c][k][d]\) be the number of times character \(d\) appears in the expansion of \(f^k(c)\). Given the counts of each character of \(c\) after \(k\) expansions, we can easily calculate the counts of each character after \(k+1\) expansions by using the values in \(T\). \(c\) and \(d\) are both bounded by 26, and we only need it for values of \(k\) less than 50. Hence this DP has complexity \(O(26\times26\times\log(K)\times50)\), and afterwards, we can query fksize(char c, int k) in constant time.

Be careful in how we handle overflowing, since theoretically, the size of any value in the DP can grow to \(\log(K)^{|T|_{max}} = 50^{50}\). The key observation is that once again, we know that any value over \(10^{15}\) is irrelevant, since \(m_i\) will always be within the first \(10^{15}\). Thus each time we add, just check if the result is over \(10^{15}\), and if so, set it back to \(10^{15}\) to avoid overflow.

Summary and Complexity

This was quite the long explanation, so I’ll summarise the algorithm one last time.

1. Use fkfirst(S[0], max(K-50, 0)) to find the first character that is depth at least 50 from the end. Let us expand this character once to obtain the string \(s\).
2. For each number \(m_i\)
   1. For each character \(s_j\) in \(s\), calculate it’s size using fksize(c, k).
   2. If \(m_i\) is in the expansion of \(s_j\), then let \(s\) be the expansion of that character, and repeat.
   3. Otherwise, subtract the size from \(m_i\) and try again on the next character \(s_{j+1}\).
   4. When we reach a leaf, then that character must be \(m_i\)

The overall complexity is \(O(26)\) for the call to fkfirst, \(O(26\times26\times\log K\times |T|_{max})\) to preprocess the DP, and then \(O(\log K \times |T|_{max} \times M)\) to go down the tree for each \(m_i\).

Coded Solution

Though the main idea is still the same, the code presented here is little inefficient and contains multiple unecessary steps (I’m not perfect, you know!). Since then, I’ve found a cleaner solution, so here are a list of the main changes.

• I used \(60\) instead of \(50\) as the estimate for \(\log K\) to be safe.
• Instead of jumping directly to the node that was \(60\) from the bottom, I instead did an unecessary binary search to find the largest \(k\) such that \(f^k(S)\)’s first digit had a subtree size greater than or equal to \(K\).
• For fksize, I forgot that the largest \(k\) it would have to handle was \(60\), so I implemented an alternate solution using matrix exponentiation to handle arbitrary \(K\) in \(\log(K)\) time.

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
typedef vector<int> vi;
#define x first
#define y second
#define pb push_back
#define all(x) x.begin(), x.end()
#define rep(i, n) for (int i = 0; i < int(n); i++)

#define INF ll(1e15 + 5)
#define MAXS 1000005
#define MAXA 26
#define MAXM 1005

// numbers are no longer relevant when they are over 1e15
// safeadd and safemult prevent any overflows when adding or multiplying.
ll safeadd(ll a, ll b) { return a+b > INF ? INF : a+b; }
ll safemult(ll a, ll b) { // assumes both a and b are non negative
    if (b == 0) return 0;
    if (LLONG_MAX / b < a) return INF;
    if (a * b > INF) return INF;
    return a * b;
}

struct Matrix {
    // matrix struct used for matrix exponentiation
    ll a[MAXA][MAXA] = {{0}};

    // matrix multiplication
    Matrix operator *(const Matrix & oth) {
        Matrix res;
        rep(i, MAXA) rep(j, MAXA) rep(k, MAXA) {
            res.a[i][j] = safeadd(
                res.a[i][j],
                safemult(a[i][k], oth.a[k][j])
            );
        }
        return res;
    }

    void zero() {
        rep(i, MAXA) rep(j, MAXA) a[i][j] = 0;
    }

    void ident() {
        zero();
        rep(i, MAXA) a[i][i] = 1;
    }

    void print(int N=26) {
        rep(i, N) {
            rep(j, N) printf("%lld ", a[i][j]); printf("\n");
        }
    }
};

struct Vector {
    // vector struct for matrix exponentiation
    ll a[MAXA] = {0};

    Vector operator *(const Matrix & oth) {
        // multiplication with matrix
        Vector res;
        rep (i, MAXA) rep(k, MAXA) {
            res.a[i] = safeadd(
                res.a[i],
                safemult(a[k], oth.a[k][i])
            );
        }
        return res;
    }

    ll sum() {
        // returns the sum of the vector
        ll sum = 0;
        rep(i, MAXA) sum = safeadd(sum, a[i]);
        return sum;
    }

    void print(int N=26) {
        rep(i, N) printf("%lld ", a[i]); printf("\n");
    }
};


Matrix matrixexp(Matrix B, ll e) {
    // matrix exponentitation
    Matrix res;
    res.ident();
    while (e) {
        if (e & 1) res = res * B;
        B = B * B;
        e >>= 1;
    }
    return res;
}

int G[26];
bool cycle[26];
bool seen[26];
int label[26]; // -1 if not set
vector<ll> cycles;
// labels all cycles, gets their lengths, and
// gets dist from every node to their cycle.
void dfs(int at) {
    if (seen[at]) return;
    seen[at] = true;
    int to = G[at];
    if (seen[to] && label[to] == -1) {
        // found a cycle
        cycle[at] = true;
        label[at] = cycles.size();
        int sz = 1;
        while (to != at) {
            sz++;
            cycle[to] = true;
            to = G[to];
            label[to] = cycles.size();
        }
        cycles.pb(ll(sz));
    } else {
        // regular branch
        dfs(to);
        label[at] = label[to];
    }
    return;
}

Matrix DP;
ll memo[26][60];
bool done[26][60];
// returns the size of string after f is applied k times.
ll fksize(char c, ll k) {
    if (k < 60 && done[c-'a'][k]) return memo[c-'a'][k];

    Vector v;
    v.a[c-'a'] = 1;
    Matrix A = matrixexp(DP, k);
    Vector res = v * A;

    ll ret = res.sum();
    if (k < 60) {
        memo[c-'a'][k] = ret;
        done[c-'a'][k] = true;
    }
    return ret;
}

// returns the first letter if char c is expanded k times.
char fkfirst(char c, ll k) {
    int at = c-'a';

    // go towards cycle
    while (!cycle[at] && k) at = G[at], k--;
    if (k == 0) return at+'a';

    // go around cycle
    ll cyclesize = cycles[label[at]];
    k %= cyclesize;

    // complete any k left
    while (k) at = G[at], k--;
    return at+'a';
}

string ts[26];

int main () {
    ios_base::sync_with_stdio(0); cin.tie(0);

    string S;
    cin >> S;
    rep(i, 26) cin >> ts[i];
    ll K, M;
    cin >> K >> M;
    vector<ll> ms(M);
    rep(i, M) cin >> ms[i];

    // generate dp matrix
    rep(i, 26) rep(j, ts[i].size()) {
        DP.a[i][ts[i][j]-'a']++;
    }

    // generate vortex graphs
    rep(i, 26) G[i] = ts[i][0]-'a';
    fill(label, label+26, -1);
    rep(i, 26) dfs(i);

    // binary search for highest k such that f^k(s)'s
    // first digit has a subtree size >= K.
    ll l = -1;
    ll r = K;
    while (l < r-1) {
        ll m = (l+r)/2;
        char c = fkfirst(S[0], m);
        if (fksize(c, K-m) >= INF) l = m;
        else r = m;
    }

    // get the string under that first character
    string s;
    ll k = l;
    if (k == -1) s = S;
    else {
        char c = fkfirst(S[0], K-k);
        s = ts[c-'a'];
    }
    k++;
    assert(K - k < 60);

    // make a copy of k and s, so we can work on a
    // fresh version for each m_i
    ll kcopy = k;
    string scopy = s;

    // for each m_i, use brute force to locate it.
    for (ll m : ms) {
        k = kcopy;
        s = scopy;
        while (k < K) {
            // find which child m_i is in
            char d = '?';
            for (char c : s) {
                ll subsize = fksize(c, K-k);
                if (subsize < m) m -= subsize;
                else { // m is in this subtree
                    d = c;
                    break;
                }
            }

            // m_i must exist somewhere in this subtree
            assert(d != '?');

            s = ts[d-'a'];
            k++;
        }
        char ans = s[m-1];
        printf("%c\n", ans);
    }
}